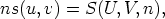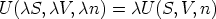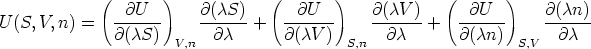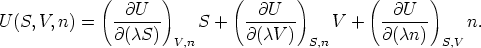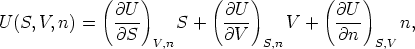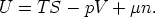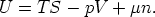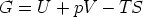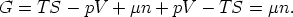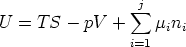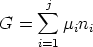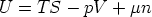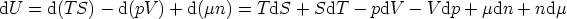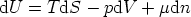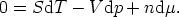The Euler Equation and the Gibbs-Duhem
Equation
Stephen R. Addison
February 25, 2003
This document was included in the TEX-showcase. This paragraph was added by
Gerben Wierda to display how TEX4ht displays the formatting of terms like
LATEX and TEX.
1 Intensive Functions and Extensive Functions
Thermodynamics Variables are either extensive or intensive. To illustrate the
difference between these kings of variables, think of mass and density. The mass of
an object depends on the amount of material in the object, the density does not.
Mass is an extensive variable, density is an intensive variable. In thermodynamics,
T, p, and 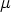 are intensive, the other variables that we have met, U, S ,
V , N, H, F, and G are extensive. We can develop some useful formal
relationships between thermodynamic variables by relating these elementary
properties of thermodynamic variables to the theory of homogeneous
functions.
are intensive, the other variables that we have met, U, S ,
V , N, H, F, and G are extensive. We can develop some useful formal
relationships between thermodynamic variables by relating these elementary
properties of thermodynamic variables to the theory of homogeneous
functions.
2 Homogeneous Polynomials and Homogeneous Functions
A polynomial
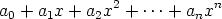
is of degree n if an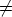 0. A polynomial in more than one variable is said to be
homogeneous if all its terms are of the same degree, thus, the polynomial in two
variables
0. A polynomial in more than one variable is said to be
homogeneous if all its terms are of the same degree, thus, the polynomial in two
variables
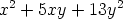
is homogeneous of degree two.
We can extend this idea to functions, if for arbitrary 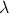
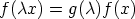
it can be shown that
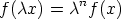
a function for which this holds is said to be homogeneous of degree n in the
variable x. For reasons that will soon become obvious 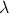 is called the scaling
function. Intensive functions are homogeneous of degree zero, extensive functions
are homogeneous of degree one.
is called the scaling
function. Intensive functions are homogeneous of degree zero, extensive functions
are homogeneous of degree one.
2.1 Homogeneous Functions and Entropy
Consider
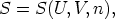
this function is homogeneous of degree one in the variables U, V , and n, where n
is the number of moles. Using the ideas developed above about homogeneous
functions, it is obvious that we can write:
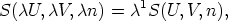
where 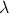 is, as usual, arbitrary. We can gain some insight into the properties of
such functions by choosing a particular value for
is, as usual, arbitrary. We can gain some insight into the properties of
such functions by choosing a particular value for 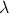 . In this case we will choose
. In this case we will choose
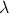 =
= 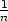 so that our equation becomes
so that our equation becomes
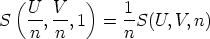
Now, we can define 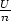 = u,
= u, 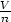 = v and S(u,v, 1) = s(u,v), the internal
energy, volume and entropy per mole respectively. Thus the equation
becomes
= v and S(u,v, 1) = s(u,v), the internal
energy, volume and entropy per mole respectively. Thus the equation
becomes
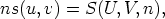
and the reason for the term scaling function becomes obvious.
3 The Euler Equation
Consider
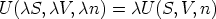
differentiating with respect to 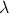 (and changing sides of the equation) this
becomes
(and changing sides of the equation) this
becomes
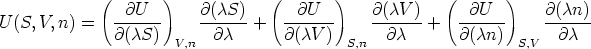
which simplifies to
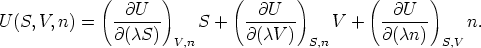
Recalling that 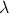 is arbitrary, we now choose
is arbitrary, we now choose  = 1, resulting in
= 1, resulting in
and recognizing that the partial derivatives in this equations are now just the
definitions of the extensive variables T, p, and n, we can rewrite this
as
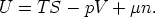
This equation, arrived at by purely formal manipulations, is the Euler equation,
an equation that relates seven thermodynamic variables.
3.1 The relationship between G and 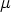
Starting from
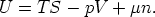
and using
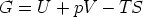
we have
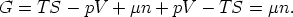
So for a one component system G = 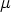 n, for a j-component system, the Euler
equation is
n, for a j-component system, the Euler
equation is
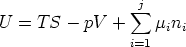
and so for a j-component system
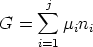
4 The Gibbs-Duhem Equation
The energy form of the Euler equation
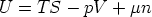
expressed in differentials is
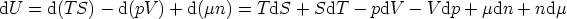
but, we know that
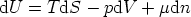
and so we find
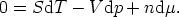
This is the Gibbs-Duhem equation. It shows that three intensive variables are not
independent - if we know two of them, the value of the third can be determined
from the Gibbs-Duhem equation.
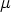 are intensive, the other variables that we have met, U, S ,
V , N, H, F, and G are extensive. We can develop some useful formal
relationships between thermodynamic variables by relating these elementary
properties of thermodynamic variables to the theory of homogeneous
functions.
are intensive, the other variables that we have met, U, S ,
V , N, H, F, and G are extensive. We can develop some useful formal
relationships between thermodynamic variables by relating these elementary
properties of thermodynamic variables to the theory of homogeneous
functions.
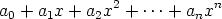
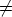 0. A polynomial in more than one variable is said to be
homogeneous if all its terms are of the same degree, thus, the polynomial in two
variables
0. A polynomial in more than one variable is said to be
homogeneous if all its terms are of the same degree, thus, the polynomial in two
variables
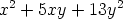
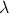
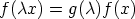
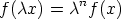
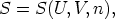
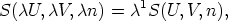
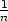 so that our equation becomes
so that our equation becomes
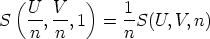
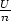 =
= 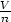 =
=